수학원리 명제의 역, 이, 대우 그리고 필요.충분 과 필요충분조건..

[도리아빠]

명제에 대하여 두번째 글입니다..^^..

첫번째 글에서 너무 복잡하고 길게 쓴 것 같아 가능한 짧고, 간단하게 적어보겠습니다..

중학수학(중2) 에서는 명제와 역 까지 교과과정이고, 이 와 대우는 고1수학에 등장 합니다..

그러나 명제를 공부할 때 중2라 하여도 같이 공부해 두는 것이 좀더 편리 합니다..

명제에 대하여는 앞의 글에서 이미 적었으니 생략하고 바로 들어가겠습니다..

명제에서 역, 이, 대우를 공부할 때 한자를 생각하면 좀더 쉽게 접근이 가능합니다..

1. 명제의 역, 이, 대우

역(易: 바꿀 역), 이(異: 다를 이), 대우(對偶: 대할 대, 짝 우)

요걸 한자의 뜻을 생각하며 본다면 그리 어렵지 않은데 각각을 예로 들어 보겠습니다..

명제(命題) : 오늘이 화요일 이면 내일은 수요일 이다, 에 대하여   p → q

역(역) : 내일이 수요일이면 오늘은 화요일 이다,                  q → p

이(이) : 오늘이 화요일이 아니면 내일은 수요일이 아니다,       ~ p → ~ q

대우(대우) : 내일이 수요일이 아니면 오늘은 화요일이 아니다,   ~ q → ~ p

이걸 보기 편하게 그림으로 표시하면 요런 식으로 됩니다..

 

명제 p → q 와 그 대우 ~ q → ~ p 는 동치관계 라 합니다..

명제 p → q 가 참이면, 그 대우 ~ q → ~ p 도 참이다.

명제 p → q 가 거짓이면, 그 대우 ~ q → ~ p 도 거짓이다

증명 : 명제 p → q 가 참이면 p, q 의 진리집합에 대하여 P⊂Q 가 성립한다..

         즉, Q^c ⊂ P^c 이고, 이때 P^c(P의 여집합), Q^c(Q의 여집합) 은 각각 조건 ~ p,~ q 의

         진리집합 이므로 ~ q → ~ p 가 참 이다..

2. 명제의 추론

p ⇒ q 이고, q ⇒ r 일 때, p ⇒ r  이다..

요렇게 두 명제 p ⇒ q, q ⇒ r 로부터 p ⇒ r 을 유도하는 추론을 삼단논법 이라 합니다..

요 삼단논법은 주로 논리학의 태두 이신 소크라테스 선생을 아주 여러 번 죽이는 것으로 많이들

이해하지요..^^..

소크라테스는 사람이다, 사람은 죽는다, 고로 소크라테스는 죽는다..

3. 필요. 충분조건과 필요충분조건

명제  p → q 가 참일 때, 즉 p ⇒ q 일 때, p 는 q 이기 위한 충분조건, q는 p이기 위한

필요조건 이라 합니다..

뭔 말 이냐 하면,

“소녀시대(p)는 가수(q) 이다” 에서, 소녀시대는 가수 이지만, 가수가 모두 소녀시대는 아니다

가수(q)는 소녀시대(p) 이기 위한 필요조건(necessary condition) 이고,

소녀시대(p) 는 가수(q) 이기 위한 충분조건(sufficient condition) 라는 말입니다..

간단히 작은놈(p)은 충분조건이고, 큰놈(q)은 필요조건 입니다..(P⊂Q)

작은놈은 큰놈에게 속할 수 있지만 큰놈은 작은놈에게 속할 수는 없지요..^^..

필요.충분 조건을 판단할 때 기호 ⇒ 가 화살의 모양을 닮았으므로 화살에서 활을 쏜는 상태를

연상하면 활시위 는 충분조건, 화살이 과녁에 맞을 때 과녁을 필요조건이라 생각하면 됩니다..

필요충분조건 이란 서로 같다는 의미를 대신 하는 표현입니다..

p ⇒ q 이고, q ⇒ p 이면 요건 동치라 하고 p ⇔ q 로 나타내며 p 는 q 이기 위한,

q 는 p 이기 위한 필요충분 조건 이라 합니다..

“해진(p) 이는 혜수 애인(q) 이다” 에서 해진 이는 혜수 애인 이고, 혜수 애인은 해진 이다..

즉, p ⇒ q 이면서, q ⇒ p 인 것이 필요충분조건 입니다..

p ⇒ q 이고, q ⇒ p 이면, P ⊂ Q, Q ⊂ P.. P = Q , p ⇔ q

사투리로 말하면 “갸가 갸가” 란 말이고, 그 놈이 그 놈이다 란 뜻입니다..^^..

요기 까지가 중2 부터 시작해서 고1 까지 배우는 명제 입니다..

사실 별로 어려운게 아닌데 말이 어려운 것 같아요..^^..

좀 풀어서 설명하면 아이들이 쉽게 이해하지 않을까 합니다..

[즐거운세상]

명제는 걍 본인이 읽고 이해하는 것이 가장 쉬운데.. 울 아들이 그게 안 되어.. 간만에 설명하느라..ㅎ 아직 다 이해되지는 않은 듯합니다. 학기 중에 채워질까요... 채워져야 할텐데...-.-

[도리아빠]

학기중에야 잘하겠지요..^^..
지금은 뭐 예습이니..

[해봅시다]

아 진짜..논리학책이 어디있나....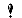

[즐거운세상]

괜찮은 책 찾으시면 저희에게도 알려주시와요~^^

[도리아빠]

ㅎㅎ..머리에 김나실려나~~..^^..

[오월동주]

아이가 어제 명제부분 공부했는데 쉬운듯 어려워하는듯해요. 참고로 읽어보라고 해야겠어요.
감사합니다.

[도리아빠]

ㅎㅎ..그냥 참조만 해보라 하세요..^^..
이걸 공부라 생각하면 또 부담이 됩니다..
감사합니다..

[로마기사]

울 아들이 집합과 명제를 이상하게 어려워 하던데 요거 프린트 해 줍니다..^^ 전 열심히 도리아빠님 올려주신거 프린트 하여 아이에게 읽어 보게 합니다. 제가 해 줄 수 있는 건 요것뿐이네요 ㅎㅎ 감사합니다^^

[도리아빠]

에고~~별말씀을요..도움이 된다면 제가 고맙지요..^^..
감사합니다..